2.6 Transition rule

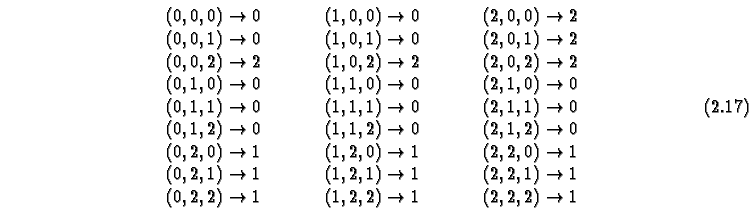
The most important aspect of a cellular automaton is the transition rule or transition function. This is what determines the evolution most. Of course the transition rule depends on the lattice geometry, the neighborhood, and the state set. Even though the transition rule most directly determines the evolution, it is in many cases not possible to predict the evolution of a CA other than by explicitly simulating it (One can prove that this is the case for those automata that can be shown to be computationally universal, such as simple automata like the ``game of life'').

2.6.1 Direct Specification

In the preceding sections we have already described several different rules in a way that seemed intuitively clear and unambiguous. In general, the transition rule can be specified in many different ways. The most direct specification is to write down the outcome of the transition rule for each possible configuration of states in the neighborhood. For the one-dimensional example automaton eq. (), page , this would be

$$\begin{array}{@{\extracolsep{1cm}}lll} (0,0,0) \rightarrow 0 & ... ...rrow 1 & (1,2,2) \rightarrow 1 & (2,2,2) \rightarrow 1 \end{array}$$

This list is very long and tedious to write down. In many cases, as in the example, the specification can be greatly simplified by the introduction of wild-cards, i.e., by indicating cases where the transition result is independent of the content of (usually) a neighbor cell. Indicating a wild-card by ``$\makebox[0.5em]{$\scriptstyle\bullet$}$'', we write the same rule as Eq. (2.10) in the shorter form

$$\begin{array}{@{\extracolsep{1cm}}ll} (0,0,0) \rightarrow 0 & (... ...akebox[0.5em]{$\scriptstyle\bullet$}) \rightarrow 0 & \end{array}$$

When specifying a transition rule in this manner, one has to take care that the specification does indeed allow a consistent and full construction of the complete table. It is this requirement that lead to the specification in Eq. (2.11) being still more complicated than the specification in Eq. (), which was intuitively clear. If we extend the definition of wild cards in such a manner that the first applicable rule takes precedence over following rules, we can simplify Eq. (2.11) to

$$\begin{array}{l} (\makebox[0.5em]{$\scriptstyle\bullet$},0,2) \... ...\makebox[0.5em]{$\scriptstyle\bullet$}) \rightarrow 0 \end{array}$$

We see that by introducing this precedence rule, we have eliminated the three rules that were listed in the second column of Eq. (2.11).

Further simplification can often be achieved by grouping states together according to the symmetries of the lattice. For the one-dimensional version with rules symmetric under reflection, we can write

$$\begin{array}{l} (2,0,\makebox[0.5em]{$\scriptstyle\bullet$}) \... ...\makebox[0.5em]{$\scriptstyle\bullet$}) \rightarrow 0 \end{array}$$

and thus obtain the same number of cases as in Eq. (). In two dimensions the implicit specification of symmetric cases is even more important. The two-dimensional rules would be

$$\begin{array}{l@{\qquad}l} \begin{array}{ccc}&2&\\ \makebox[0.5... ...5em]{$\scriptstyle\bullet$}&\end{array} \rightarrow 0 \end{array}$$

where the first rule is also valid for all copies of the configuration obtained by rotation on the lattice. This description by four lines should be contrasted to the size of the full table, which is $3^5 = 243$. Thus we have reduced the description to the essential parts.

This type of description is used in the ``GUI''-Approach to specifying rules in the JCASim system. Other descriptions use special languages, such as CDL or Java for specifications (see Chapter 3).

2.6.2 Multi-step rules

In many cases it is convenient both for the specification and for the implementation to split the automation rule into several sub-steps. This is only a practical considerations: in theory, the sub-steps can be combined into a table or rule for the whole step. We will encounter many examples of rules consisting of several sub-steps, especially the class of lattice gas automata (Chapters  and ). For our example automaton, we demonstrate this in another version of the two-variable rule Eq. (), where we include diffusion effects in variable $v$: Step 1 calculates the sum in the neighborhood of variables $u$ and $v$ separately: In principle, the neighborhoods for calculating $u$ and $v$ can be different (for more details see Chapter ). 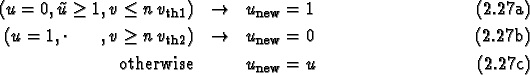Step 2 calculates the new value of $u$ from $u$, $\tilde u$ and $v$, with $n$ being the number of cells in the neighborhood for $v$ (which includes the cell to be updated): and step 3 calculates the new value of $v$: Of course we could write down the combined effect of steps 1 through 3 in one explicit step, but it is often more convenient to use this stepwise formulation, even if the actual simulation uses fewer separate steps.

In JCASim such multistep rules use global vaiables which control the stepping.

2.6.3 Probabilistic rules

An important class of transition rules are probabilistic rules. In this case the transition rule is not a function which has exactly one result for each neighborhood configuration, but a rule that provides one or more possible outcomes with associated probabilities. Of course the sum of probabilities of all outcomes must be one for each input configuration. The probabilistic choices of all cells are independent of one another (uncorrelated). Formally this is described by stating the transition function as

$$G: S^n \times S \rightarrow [0,1],$$

i.e., a function that for each input configuration assigns a real number to each output, which gives the probability for this output. To obtain correct probabilities, the sum of probabilities for all outcomes, given an input configuration, must be one:

$$\forall \{s_i\}_{i=1}^n\ :\ \sum_{s'} G(\{s_i\}, s') = 1$$

Usually, $G$ is nonzero for only a few values of $s'$.

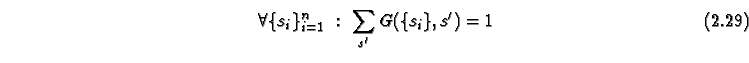
The introduction of probabilistic rules is very important in many modeling situations, since many natural systems are noisy. In some cases it is sufficient to introduce random initial conditions, which also lead to a noisy or random behavior. But in many cases probabilistic rules have advantages.

Applet 2.17: Probabilistic rules with $n=10$. Evolution from an initial point, showing every second time step.
Let us demonstrate the effects of introducing probabilistic rules in our example. We use the following rule with $n=10$ ($p$ is the probability): 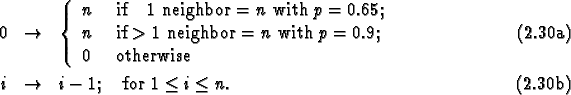The effect of the probabilistic rules is that wavefronts do not remain flat, and do not propagate at full speed, since infection does not always take place. Figure 2.17 shows the evolution of an initial small excited region. We observe that the wave front is irregular, but more circular than with deterministic rules (A detailed investigation into different ways to achieve good isotropy in cellular automata can be found in [5]). We also observe (in the second row) that the wave front has broken up, and propagates back into the interior. We have selected the version with $n=10$ because for $n=1$ this phenomenon happens very often, and is less easy to recognize.

We will encounter several examples of cellular automata with probabilistic rules in the later chapters, and also discuss how to simulate a probabilistic automaton into a deterministic automaton by integrating a random number generator in the CA rules.