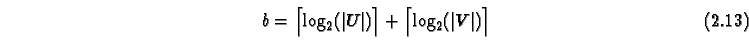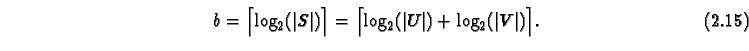According to the definition of cellular automata, each cell is a finite
automaton, and therefore the set of states has finite size. In addition, the
set is usually fairly small. There are several reasons for this. People have
investigated all possible CAs with a given number of states and a given
neighborhood size [7]. This is only possible when the set of states is very small,
since the number of possible CAs with ![]() states and
states and ![]() cells in the
neighborhood (including the cell to be updated), is
cells in the
neighborhood (including the cell to be updated), is ![]() .
This number rapidly becomes too big to explore all possibilities as
.
This number rapidly becomes too big to explore all possibilities as ![]() and
and ![]() grow:
grow:
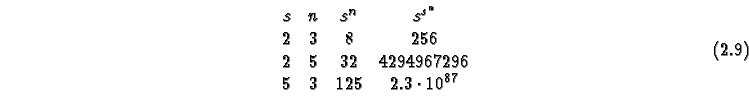
The second reason to prefer small state sets, and which is more important for
simulation, is that only when there are few states is it possible to specify the CA rules explicitly and store them in a table (the table size is ![]() )
)
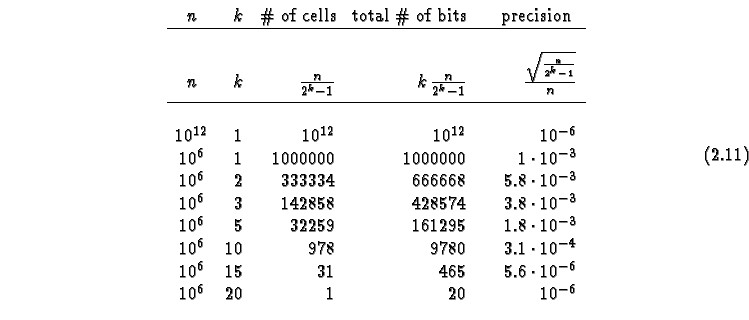
A reason to use large numbers of states can be that a CA can better approximate a continuous system with more states. This can be seen by considering the representation of ![]() particles in a CA. Using a CA with one bit per cell, we need
particles in a CA. Using a CA with one bit per cell, we need ![]() cells. When particles are placed randomly in these cells, the fluctuations in particle number in a subset of cells are
cells. When particles are placed randomly in these cells, the fluctuations in particle number in a subset of cells are ![]() . Therefore the precision is
. Therefore the precision is ![]() . On the other hand, with
. On the other hand, with ![]() bits per cell,
bits per cell, ![]() particles can be represented in each cell. Therefore only
particles can be represented in each cell. Therefore only ![]() cells are needed, and the fluctuations are
cells are needed, and the fluctuations are ![]() . Thus the precision is
. Thus the precision is 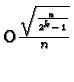 . For different choices
. For different choices
Even though a simulation using floating-
point variables is still using a finite set of states
(about ![]() states for a single-precision floating point variable),
we should not call such models cellular automata. Such programs are usually
a computer approximation of models using real, i.e., continuous numbers,
and the discretization is not very well controlled. For models with real
variables the names coupled map lattice (CML) [3,2]
or finite difference method for PDEs might be appropriate.
The simulation system JCASim does allow such models, but not all transformations
are available in this case.
states for a single-precision floating point variable),
we should not call such models cellular automata. Such programs are usually
a computer approximation of models using real, i.e., continuous numbers,
and the discretization is not very well controlled. For models with real
variables the names coupled map lattice (CML) [3,2]
or finite difference method for PDEs might be appropriate.
The simulation system JCASim does allow such models, but not all transformations
are available in this case.
Let us explore changing the state set in our example. One possibility is to use ![]() states and generalize the rules to
states and generalize the rules to
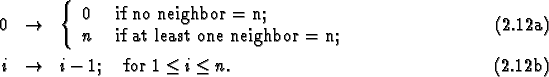 This rule leads to a longer refractory period for
This rule leads to a longer refractory period for ![]() .
Figure 2.16 shows
an example with
.
Figure 2.16 shows
an example with ![]() .
.
Applet 2.16: Example automaton with ![]() .
.
A common construction of CAs is to have several variables in each cell that
must be stored in the state. In this case we construct the state set ![]() as
the cross-product of the sets for each variable.
as
the cross-product of the sets for each variable.
Formally the state set is described as ![]() , where
, where ![]() and
and ![]() are the set of values which the variables
are the set of values which the variables ![]() and
and ![]() can take. The size
of the set
can take. The size
of the set ![]() is
is ![]() . Often it is more practical to count
the number of bits needed to represent the state
. Often it is more practical to count
the number of bits needed to represent the state