


Next: 2.5 State set
Up: 2. Choices in the
Previous: 2.3 Boundary conditions
Contents
2.4 Initial conditions
Not only the boundary conditions need to be specified, but also the initial
condition. In most cases the initial condition determines very much the
subsequent evolution. Initial conditions can be very special (constructed),
or they can be generated randomly.
One important consideration in the generation of initial conditions is that
many cellular automata rules conserve some quantities. This can be for example
the total number of particles, the total momentum, or energy. It can also
be some spurious conserved quantities, i.e., quantities that are not conserved
in the system to be modeled, e.g., the number of particles in one row/column.
In generating initial conditions, care must be taken that the intended value
for the conserved quantities is reached (especially with random initial
conditions), and that the spurious conserved quantities do not generate
undesired effects.
We have already seen examples of special constructed initial conditions
for the example automaton: In Figure ![[*]](cross_ref_motif.gif) we started with
one excited cell (state=2) in a background of quiescent cells (state=0).
In Figure 2.3 we started with half a row of excited
(state=2) cells, followed by half a row of recovering (state=1) cells in a
background of quiescent cells (state=0). This special initial condition,
which is constructed to represent a wavefront that is cut off and placed
in quiescent medium, leads to the development of a spiral wave.
we started with
one excited cell (state=2) in a background of quiescent cells (state=0).
In Figure 2.3 we started with half a row of excited
(state=2) cells, followed by half a row of recovering (state=1) cells in a
background of quiescent cells (state=0). This special initial condition,
which is constructed to represent a wavefront that is cut off and placed
in quiescent medium, leads to the development of a spiral wave.
Now we show the evolution from random initial conditions: If we start with
a proportion of 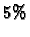 cells in state
cells in state 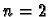 , and all others in state
, and all others in state 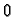 ,
we see in Figure 2.14
that the evolution leads to expanding waves around each seed, which
annihilate each other when they meet.
,
we see in Figure 2.14
that the evolution leads to expanding waves around each seed, which
annihilate each other when they meet.
Applet 2.14:
Example automaton with random initial conditions
(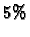 2-cells).
2-cells).
If we start with a proportion of 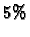 cells in state
cells in state 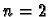 ,
another
,
another 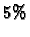 cells in state
cells in state 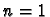 , and all others in state
, and all others in state 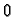 ,
we see in Figure 2.15
a similar evolution. The only difference appears for cases
where a cell with value
,
we see in Figure 2.15
a similar evolution. The only difference appears for cases
where a cell with value 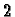 and a cell with value
and a cell with value 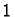 lie next to
each other, for in this case a center emitting periodic waves is
created (two centers in lower right Figure 2.15). In the
deterministic Greenberg-Hastings automaton, the number of spiral waves
or spiral wave pairs is a conserved quantity.
lie next to
each other, for in this case a center emitting periodic waves is
created (two centers in lower right Figure 2.15). In the
deterministic Greenberg-Hastings automaton, the number of spiral waves
or spiral wave pairs is a conserved quantity.
Applet 2.15: Example automaton with random initial conditions (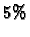 2-cells and
2-cells and 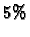 1-cells).
1-cells).



Next: 2.5 State set
Up: 2. Choices in the
Previous: 2.3 Boundary conditions
Contents
Jörg R. Weimar
![[*]](cross_ref_motif.gif) we started with
one excited cell (state=2) in a background of quiescent cells (state=0).
In Figure 2.3 we started with half a row of excited
(state=2) cells, followed by half a row of recovering (state=1) cells in a
background of quiescent cells (state=0). This special initial condition,
which is constructed to represent a wavefront that is cut off and placed
in quiescent medium, leads to the development of a spiral wave.
we started with
one excited cell (state=2) in a background of quiescent cells (state=0).
In Figure 2.3 we started with half a row of excited
(state=2) cells, followed by half a row of recovering (state=1) cells in a
background of quiescent cells (state=0). This special initial condition,
which is constructed to represent a wavefront that is cut off and placed
in quiescent medium, leads to the development of a spiral wave.