4.3 Coding as a logic function

In the preceeding section we have seen how the transition function can be translated into a lookup-table. In this section we describe a transformation of this table into a set of logical formulas. The table can be regarded as a function

$$\begin{eqnarray} f: [0 \cdots 2^k-1] &\mapsto& [0 \cdots 2^n-1]\\ f(x) &=& y \end{eqnarray}$$

where $k$ is the number of input bits, and $n$ is the number of output bits (usually also the number of bits in the cell state). Alternatively, consider the binary representation of $x$ and $y$:

$$\begin{eqnarray} x &=& \sum_{i=0}^{k-1} 2^i \ x_i \\ y &=& \sum_{j=0}^{n-1} 2^j \ y_j \end{eqnarray}$$

and decompose the function $f$ into boolean functions

$$g_j(x_0,x_1,\cdots,x_{k-1}), \qquad j = 0,\cdots,n-1$$

such that

$$f(x) = y = \sum_{j=0}^{n-1} 2^j \ g_j(x_0,x_1,\cdots,x_{k-1}).$$

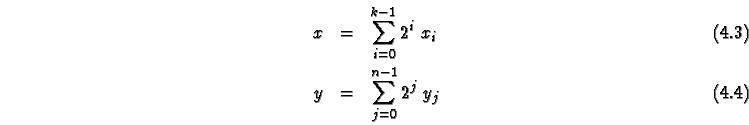
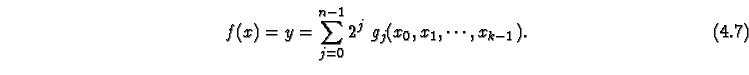
We can now try to find a compact representation of the functions $g_j$ in terms of the logical functions available on a computer, namely AND (&), OR (|), NOT (~), XOR (^).

4.3.1 Logic minimization

The task here is to find a compact representation of a set of boolean functions which are given as a set of input values, for which the output (the $j$th bit in the table output) is 1 (true). There are several approaches to this problem. Older methods, such as the Quine-McCluskey procedure or the approach used in the espresso software package [] aimed to produce a minimal two-level representation, e.g., as a disjunctive minimal form. In the case of a computer code implementing the logic function, where operations are applied sequentially, a representation using more levels does not carry a performance penalty, and is most likely more compact. Such a representation can best be found by algorithms that manipulate a data structure called binary-decision-diagram or BDD.

4.3.2 Using BDDs to find a compact representation

Binary decision diagrams (BDDs) [,] are a graph-based representation of boolean functions. A node in the BDD is labeled by a variable of the boolean function. The node represents the Shannon decomposition of a function with the cofactors $f_{low}$ and $f_{high}$ represented by the two child nodes $v_{low}$ and $v_{high}$ of node $v$. Two terminal nodes labeled 0 and 1 represent the constant functions 0 and 1. The BDDs we consider here are ordered, that is, the variables occur at most once in each path and in the same order in all paths from the roots to the terminal nodes.

x0

~x0

x0 & x1

x0 | x1

x0 ^ x1

(x0 ^ x1) & ~x2

99#1

Figure 4.1 shows the BDD representation of a number of simple boolean functions. A binary decision diagram can be reduced by the following two operations:

• Type 1: If two subgraphs are isomorphic, they are identified.
• Type 2: If the two cofactors of a node are identical, i.e., the 100#2 and the 101#3 child of the node are identical, this node can be deleted and all references to this node can be replaced by references to the child node.

The result of applying these two operations to a fixed point leads to a reduced graph. For a given variable ordering, this graph is a unique representation of the boolean function. Efficient algorithms exist for the manipulation of such a BDD []. One such operation is the reordering of the variables, which is most easily achived by the exchange of two adjacent variables in the ordering.

4.3.2.1 Minimization of BDDs

The size of a BDD depends very much on the variable ordering. Therefore one necessary optimization step is to find a good ordering which leads to a small number of nodes in the graph. The task to find the best ordering has exponential running time (since there are 102#4 different orderigs of $n$ variables). An alternative is the sifting algorithm: In this approach th evariables are orderd by the number of nodes label with each variable (The level size). The the variable with the largest level size is shifted to all possible positions, and the psition which results in the smallest overall BDD size is kept. This operation is then repeated for the other variables. The disadvantage of this algorithm is that closely coupled variable can prevent the algorithm from finding a good ordering, since only one variable can be shifted at a time, and the other closely coupled variables can prevent it from moving away in the variable ordering.

An alternative is the window permutation algorithm: Here a window size is selected (e.g., 4) and this window is shifted over the variables. Within the window all permutations of the variables in this window are tested (Window size 4: 24 permutations), and the best permutation is kept. The window is then shifted by one position an the process repeated. If during one pass of this algorithm an improvement occurred, the algorithm is repeated. The permutations are arranged in such a way that two successive permutations are related by an exchange of two neighboring variables. Examples:

• Window size 2: (0,1) - (1,0).
• Window size 3: (0,1,2) - (1,0,2) - (1,2,0) - (2,1,0) - (2,0,1) - (0,2,1) .
• Window size 4: (0,1,2,3) - ( 1,0,2,3) - (1,2,0,3) - (1,2,3,0) - (2,1,3,0) - (2,1,0,3) 103#5

As a result, this algorithm leads to simplified BDD in most cases with a reasonable computational effort. A practical example can be found in Figure 4.3.

4.3.2.2 Mapping into program code

Usually BDDs are used in the verification of logical circuits (where the uniqueness of the representation is important) or in the synthesis of circuits. In this circumstance, the process of creating logical gates from the BDD is called technology mapping. In our case, we want to generate Java code with the logical operators available in the Java language, which are AND (&), OR (|), NOT (~), and XOR (^). The code should store common subexpressions in temporary variables and generate one expression for each output bit of the multivalued function. One possible approach is to directly translate the BDD according to the definition and generate code such as ( (~xi & xi_low ) | (xi & xi_high ) for node 104#6 with childs 105#7 and 106#8, where xi_low would be the expression resulting from the translation of node 105#7. This approach can be simplified by recognizing common patterns and translating them directly into more efficient code. Figure 4.2 shows some patterns recognized. The following table contrasts the long version of all recognized patterns with the reduced code:

107#9

=108#10

xi

=109#11

~xi

=1.5110#12

xi & y

=1.5111#13

xi | y

=1.5112#14

~xi & y

=1.5113#15

~xi | y

=2114#16

xi ^ f(xk,y)

115#17

Figure 4.3: Bdd for the example program T4. On the left, the initial variable ordering produces a Bdd with 29 nodes, while the permutation search produces a variable ordering, for which the Bdd has only 17 nodes (right).

116#18

4.3.3 Storing a CA for logic coding

The logic representation of a transition table can be directly applied to the cell state as it is stored in the table upfdate method. In this case the different input bits are extracted from the address calculated for the table:

    int in0 = ((adr>>0)&1);
    int in1 = ((adr>>1)&1);
    .....
    int in6 = ((adr>>6)&1);

Then the logic function is applied, which calculates the output bits out0, out1, 103#5 , out117#19, which are then combined to yield the new state

    mystatetable = out0  | (out1<<1) | (out2<<2);

In the example the automatically produced logic function is

    int t0 = ~in2;
     out0 =  ((~in3 & in4) | (in3 & (in0 ^ in4)));
     out1 =  ((~in3 & in1) | (in3 & ((~in0 & in1) 
     	| (in0 & ((~in4 & in1) | (in4 & (in5 ^ in2)))))));
     out2 =  ((~in3 & in2) | (in3 & ((~in0 & in2) 
     	| (in0 & ((~in4 & in2) | (in4 & ((~in5 & in6) 
	| (in5 & (in6 ^ in2)))))))));

while manual simplification is much too complicated already in this small example.

Of course the resulting transition function is much more complex than a simple table lookup, and therefore is very inefficient. The only case where it might be competitive is where the table is very large, memory access is very slow but the logic representation is short and logic operations are very fast.

4.3.4 Multispin storage

Fortunately, there exists an alternative storage scheme for which the logic coding is very efficient. Not ethat the logic function in the naive storage scheme used above uses only one bit of the integers used for the calculation. But the logic operations used here have the property that they operate on all 32 or 64 bit sof an integer in parallel and without interference between one bit and another (unlike operations such as + and *, which do generate carry bits). We can use this property and store th einformation of 32 or 64 cells in one integer. Then one application of the logic function updates 32 or 64 cells in parallel, which more than offsets the inefficiency of the logic coding. In the 1-D example, the declaration for the memory reads

    int data[(lx+63)/64][k];

where k is the number of bit sneeded for storig the cell state, and 118#20 is the size of the CA. Then the inputs for the transition function are

    long in0 = mysOld[x][0];
    long in1 = mysOld[x][1];
    long in2 = mysOld[x][2];
    long in3 = (mysOld[x][0]>>>1);
    long in4 = (mysOld[x][0]<<1);
    long in5 = (mysOld[x][1]<<1);
    long in6 = (mysOld[x][2]<<1);

As you can see, in0 103#5 in2 are accessing the cell itself, while accesses to neighboring cells translate to a shift of the integer. Note that those cells which lie at the border of a 32/64 cell block need special care for those neighbors which lie on adjacent blocks. In this case the following code is added:

    if (x < numberOfLongs-1){
        in4 |= ((mysOld[x+1][0]>>63)& 0x1L);
        in5 |= ((mysOld[x+1][1]>>63)& 0x1L);
        in6 |= ((mysOld[x+1][2]>>63)& 0x1L);
    }
    if (x > 0){
        in3 |= (mysOld[x-1][0]<<63);
    }

The coding style described here is only applicable on the level of a lattice, since it groups different cells together. This is realized in the simulation system by generating a special subclass of the Lattice class which implements the state transition function itself instead of calling the method transition of the State objects. The result is a performance which for some rules is comparable to the performance of native C code, and is 10 times faster than any other Java coding style.