


Next: 4.3 Coding as a
Up: 4. Efficient simulation of
Previous: 4.1 Translating CDL to
Contents
Subsections
A cellular automaton in the classical definition is a regular lattice of cells,
each of which contains a state selected from a finite set of states.
The cells are updated according to a state transition function depending on a
finite number of neighbors of each cell. Since both the set of states and the
neighborhood are finite, the number of different possible local configurations
which can occur as inputs to the state transition function is also finite. If
this number is small enough, we can store the result of the local state
transition function in a table, and use this table in the simulation instead of
the (translated) transition function.
The translation process proceeds along the following steps in the CASim system:
First, the system collects the list of variables used as inputs to the state
transition function. These are just those components of the state of the cell
and of its neighbors, which appear as read-accesses in the transition function.
In many cases the relevant configuration does not contain all parts of the state
for all neighbors, but just one or a few components of a neighbor's state.
From the list of accessed (neighboring) state variables the size of the input
configuration is determined: For each distinct part, the number of bits used to
store this state component are calculated, and these numbers are added for all
parts of the active neighborhood.
If the result is at most 22 bits, this means that the look-up table has at most
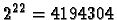 entries, which makes it feasible to store the entire table,
and also makes it possible to store the entire state of a cell in one integer
variable.
entries, which makes it feasible to store the entire table,
and also makes it possible to store the entire state of a cell in one integer
variable.
In order to use a look-up table, a method must be found to calculate an index
into the table (address) from the local configuration. For the calculation,
each active neighborhood component is assigned a bit-mask and a shift for
composition into an address. For the example T1 from section
4.1, the following properties are calculated:
![\begin{tabular}{cccccc}
name & size (bits) & mask & shift1 & shift2 \\ \hline
\v...
...\verb*!*[ 1].a! & 1 & 1 & - & 4\\
\verb*!*[ 1].b! & 2 & 6 & - & 4
\end{tabular}](img79.gif)
Here shift1 is the bit position of this component in the integer
representation of the state. shift2 is the shift needed to place the bit
pattern masked by the mask into the address for access to the look-up table.
The address is calculated as the disjunction of expressions of the form
(name & mask )<< shift2 for each component of the active neighborhood, in
this example:
int adr = (*[0] & 7)
| ((*[-1] & 1)<<3)
| ((*[ 1] & 1)<<4)
| ((*[ 1] & 6)<<4);
where the first line collects all relevant components of the cell itself,
and the other lines refer to the neighbors.
To fill the look-up table, we use the state transition function translated into
Java in the normal way. We set up a special Cell object which
is given an index of the table and
provides the appropriate states as neighbors. The transition-method of the
original java class is then
called once to update the state. The resulting state is converted into an
integer (using the mask and local shifts calculated before), and stored in
the table. Even though this process must be performed for each table entry, it
takes at most a few seconds.
Finally, a new Java class is generated which uses the look-up table in the state
transition function, but otherwise behaves exactly as before (e.g., for
initialization and display). This is achieved by subclassing the previously
translated state-class. The transition-method is overridden, and
additional methods are provided for conversion between the representation using
one integer and the representation using seperate variables for the state
components.
Example:
public class T4Table extends T4 {
protected int mys;
static final int table[] = {
0,0,2,2,4,4,6,6,0,1,2,3,4,5,6,7
.......
,1,1,3,3,5,5,7,7,1,6,3,6,5,0,7,0
};
public void transition(Cell cell){
final State [] neighbors = cell.getNeighbors();
int adr = (mys & 7)
| ((((T4Table)neighbors[1]).mys & 1)<<3)
| ((((T4Table)neighbors[2]).mys & 1)<<4)
| ((((T4Table)neighbors[2]).mys & 6)<<4)
;
mystatetable = table[adr];
}
private void toOriginal(){
mystate.a = (((mys & 1) >> 0)==1);
mystate.b = (((mys & 6) >> 1));
}
private void toTable(){
mys = ((mystate.a?1:0) << 0)
| ((mystate.b) << 1) ;
}
.....
The translation from CDL and Java code into the table form has a number of
limitations. Most importantly, the size of the active neighborhood may not be
too large, since tables targer than about 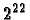 entries are impractical to
generate and to store. A second limitation is that probabilistic rules are
difficult to handle. If only one binary probabilistic choice appears in the
transition function, and this choice has a fixed probability (as opposed to a
data-dependent probability), then thi schoice can be incorporated as an extra
input bit in th etransition table, and a bit with the appropriate statistics can
be generated for each table-lookup operation. This approach only extends to a
few binary choices or one probabilistic choice with very few alternatives and no
data dependency. Otherwise, the table would become prohibitively large.
entries are impractical to
generate and to store. A second limitation is that probabilistic rules are
difficult to handle. If only one binary probabilistic choice appears in the
transition function, and this choice has a fixed probability (as opposed to a
data-dependent probability), then thi schoice can be incorporated as an extra
input bit in th etransition table, and a bit with the appropriate statistics can
be generated for each table-lookup operation. This approach only extends to a
few binary choices or one probabilistic choice with very few alternatives and no
data dependency. Otherwise, the table would become prohibitively large.
Obviously, the table method is not applicable to cell states that contain
floating-point numbers or integers without range limitation.



Next: 4.3 Coding as a
Up: 4. Efficient simulation of
Previous: 4.1 Translating CDL to
Contents
Jörg R. Weimar
![\begin{tabular}{cccccc}
name & size (bits) & mask & shift1 & shift2 \\ \hline
\v...
...\verb*!*[ 1].a! & 1 & 1 & - & 4\\
\verb*!*[ 1].b! & 2 & 6 & - & 4
\end{tabular}](img79.gif)
![\begin{tabular}{cccccc}
name & size (bits) & mask & shift1 & shift2 \\ \hline
\v...
...\verb*!*[ 1].a! & 1 & 1 & - & 4\\
\verb*!*[ 1].b! & 2 & 6 & - & 4
\end{tabular}](img79.gif)