 |
For a CA to be reversible, the global state transition function has to be reversible. For this, it has to be a permutation, so that each global state has exactly one successor and exactly one predecessor. In general, it is very difficult to verify this property for a given CA, especially since it has to be verified for all possible sizes of the CA. In order to facilitate the construction of reversible CA, we can introduce constructions that ensure the reversibility of the global state transition function given some local properties. For general CA this is not possible, since the state transition function uses information from the neighbors (see Figure 2.18), and this information flow is not easily reversible.
 |
The transition function ![]() now is a function
now is a function ![]() , where
, where ![]() is
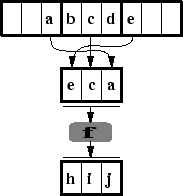
the complete state of a cell, which is assembled from the parts of the different
neighbors. The complete updating step consists of two parts: assembling the
partitions from the neighborhood and then application of
is
the complete state of a cell, which is assembled from the parts of the different
neighbors. The complete updating step consists of two parts: assembling the
partitions from the neighborhood and then application of ![]() . The first part is
clearly reversible, since it is globally a permutation of the parts of the cells
(assuming the boundary conditions are set correctly). If the second part is also
reversible, i.e., if
. The first part is
clearly reversible, since it is globally a permutation of the parts of the cells
(assuming the boundary conditions are set correctly). If the second part is also
reversible, i.e., if ![]() is a permutation, then the whole CA is reversible by
simply reversing
is a permutation, then the whole CA is reversible by
simply reversing ![]() and exchanging the order of the two substeps.
and exchanging the order of the two substeps.
This concept of partitioned CA is also used in the lattice gas cellular
automata, even for cases that are not reversible. In this case the function ![]() is not reversible, or it is probabilistic. Nevertheless, the partitioning in this
case helps ensure the conservation of mass (particle numbers):
The partitioning step conserves particles (here: bits) by definition, and the
function
is not reversible, or it is probabilistic. Nevertheless, the partitioning in this
case helps ensure the conservation of mass (particle numbers):
The partitioning step conserves particles (here: bits) by definition, and the
function ![]() is constructed to do so, too.
is constructed to do so, too.
Partitioned CA can be constructed for any dimension, lattice geometry, and
neighborhood size. The state set is a product set of ![]() sets, where
sets, where ![]() is the
size of the neighborhood. The parts of the state need not be equal in size.
is the
size of the neighborhood. The parts of the state need not be equal in size.
It is trivial to see that partitioned CA are real CA in the strict sense of the definition, since they are just a restricted subset. On the other hand, normal CA can be simulated by partitioned CA by expanding the state set, and just replicating the state of a cell in each part, so that each neighbor sees a replicated version of the cell's state.
As an example, we can use a partitioned CA to simulate a one-dimensional
excitable medium. Of course, the excitable medium is by its nature irreversible,
so we use an irreversible function ![]() . Figure 2.20 shows the
function
. Figure 2.20 shows the
function ![]() we use, together with an example evolution. In the evolution, both
the partitioning step and the function application are shown. The function is
constructed to show left- and right moving waves, which annihilate each
other when they meet.
we use, together with an example evolution. In the evolution, both
the partitioning step and the function application are shown. The function is
constructed to show left- and right moving waves, which annihilate each
other when they meet.
 |
A well-known class of partitioned CA are the Lattice Gas Automata (LGA).
One problem is that the state set is relatively large. A partitioned CA with ![]() neighbors has to use at least
neighbors has to use at least ![]() bits, i.e.,
bits, i.e., ![]() states. Therefore we cannot
construct a partitioned CA with only two states.
states. Therefore we cannot
construct a partitioned CA with only two states.
The block CA [4] provides an alternative: Partition the cells of a CA into a regular pattern of blocks that cover the whole space and do not overlap. Then apply a transformation function to each block synchronously and independently. This provides interaction of the cells within a block. But how do cells communicate across block boundaries? Simply shift the block boundaries for the next step. In this way the new block spans the block boundary of the precious step. Figure 2.21 illustrates this with a one-dimensional CA.
In block CA the local updating function is a function ![]() .
Again, the construction of a reversible CA relies on the reversibility of the
partitioning and of
.
Again, the construction of a reversible CA relies on the reversibility of the
partitioning and of ![]() . The partitioning does not change or even move any bits,
and therefore it is reversible. If the function
. The partitioning does not change or even move any bits,
and therefore it is reversible. If the function ![]() is a permutation, it is also
reversible and so the block CA is reversible. It is also simple to construct
irreversible CA with conservation laws using the concept of block CA.
is a permutation, it is also
reversible and so the block CA is reversible. It is also simple to construct
irreversible CA with conservation laws using the concept of block CA.
Are block CA real CA? Normal CA have state transition function ![]() and not
and not ![]() . Nevertheless it is possible to
simulate block CA with ordinary CA (by collecting all states of a block within
one cell) and vice versa, so block CA are equivalent to ordinary CA.
Of course this theoretical equivalence does not say much about the practicality
of the different approaches. Block CA are very useful in situations where the
state of a cell should be only one bit, but a (partial) conservation law holds.
They can also be used in situations where a strong exclusion principle is
combined with a conservation law.
. Nevertheless it is possible to
simulate block CA with ordinary CA (by collecting all states of a block within
one cell) and vice versa, so block CA are equivalent to ordinary CA.
Of course this theoretical equivalence does not say much about the practicality
of the different approaches. Block CA are very useful in situations where the
state of a cell should be only one bit, but a (partial) conservation law holds.
They can also be used in situations where a strong exclusion principle is
combined with a conservation law.