


Next: 2.3 Boundary conditions
Up: 2. Choices in the
Previous: 2.1 Lattice geometry
Contents
Once the lattice is decided upon, we choose a neighborhood in which
cells can interact. In the examples used so far, we have used the nearest neighbors only.
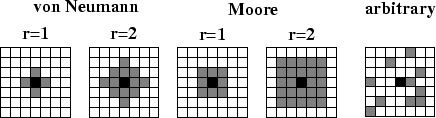
The neighborhood is described by giving the set of cells that neighbor a given cell 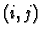 . For the nearest neighbors on a square lattice, the neighborhood, which is called the von-Neumann neighborhood, is described by
. For the nearest neighbors on a square lattice, the neighborhood, which is called the von-Neumann neighborhood, is described by
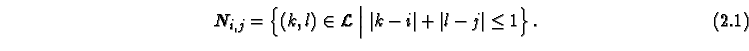
Other common neighborhoods are the Moore neighborhood
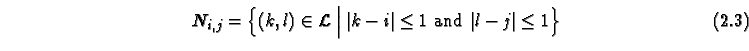
and the obvious generalizations of the von-Neumann neighborhood to radius 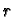 ,
,
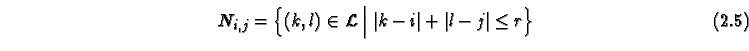
and the Moore neighborhood to radius 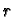 ,
,
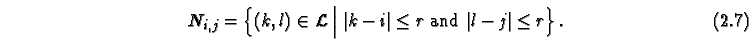
Of course, any other neighborhood can be defined (as long as it is uniform and finite).
The mentioned neighborhoods are shown in Figure 2.6,
Figure 2.6:
Examples for the different neighborhoods.
 |
and the evolution of our example automaton with different neighborhoods is shown in
Figures 2.7 and 2.8 (to be compared to Figure ![[*]](cross_ref_motif.gif) ). In this case the choice of the neighborhood affects the speed of wave propagation and the shape of the waves.
In combination with a modification of the rules, the extension of the neighborhood sometimes leads to much better isotropy, and is therefore often used when natural phenomena are to be modeled. Note that a large neighborhood is usually very inefficient to simulate.
). In this case the choice of the neighborhood affects the speed of wave propagation and the shape of the waves.
In combination with a modification of the rules, the extension of the neighborhood sometimes leads to much better isotropy, and is therefore often used when natural phenomena are to be modeled. Note that a large neighborhood is usually very inefficient to simulate.
Applet 2.7: Example automaton using the Moore
neighborhood with 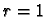 .
.
Applet 2.8: Example automaton using the von Neumann
neighborhood with 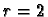 .
Note that the wave spreads with a speed of 2 cells per time step.
.
Note that the wave spreads with a speed of 2 cells per time step.



Next: 2.3 Boundary conditions
Up: 2. Choices in the
Previous: 2.1 Lattice geometry
Contents
Jörg R. Weimar
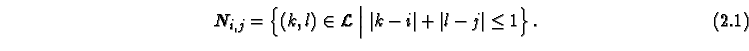
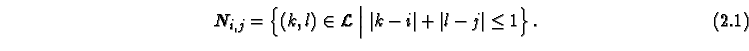
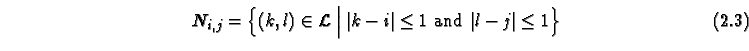
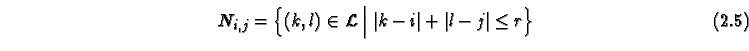
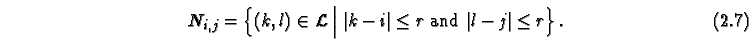
![[*]](cross_ref_motif.gif) ). In this case the choice of the neighborhood affects the speed of wave propagation and the shape of the waves.
In combination with a modification of the rules, the extension of the neighborhood sometimes leads to much better isotropy, and is therefore often used when natural phenomena are to be modeled. Note that a large neighborhood is usually very inefficient to simulate.
). In this case the choice of the neighborhood affects the speed of wave propagation and the shape of the waves.
In combination with a modification of the rules, the extension of the neighborhood sometimes leads to much better isotropy, and is therefore often used when natural phenomena are to be modeled. Note that a large neighborhood is usually very inefficient to simulate.
![]() .
.
![]() .
Note that the wave spreads with a speed of 2 cells per time step.
.
Note that the wave spreads with a speed of 2 cells per time step.